Dominik Císař | FRACT

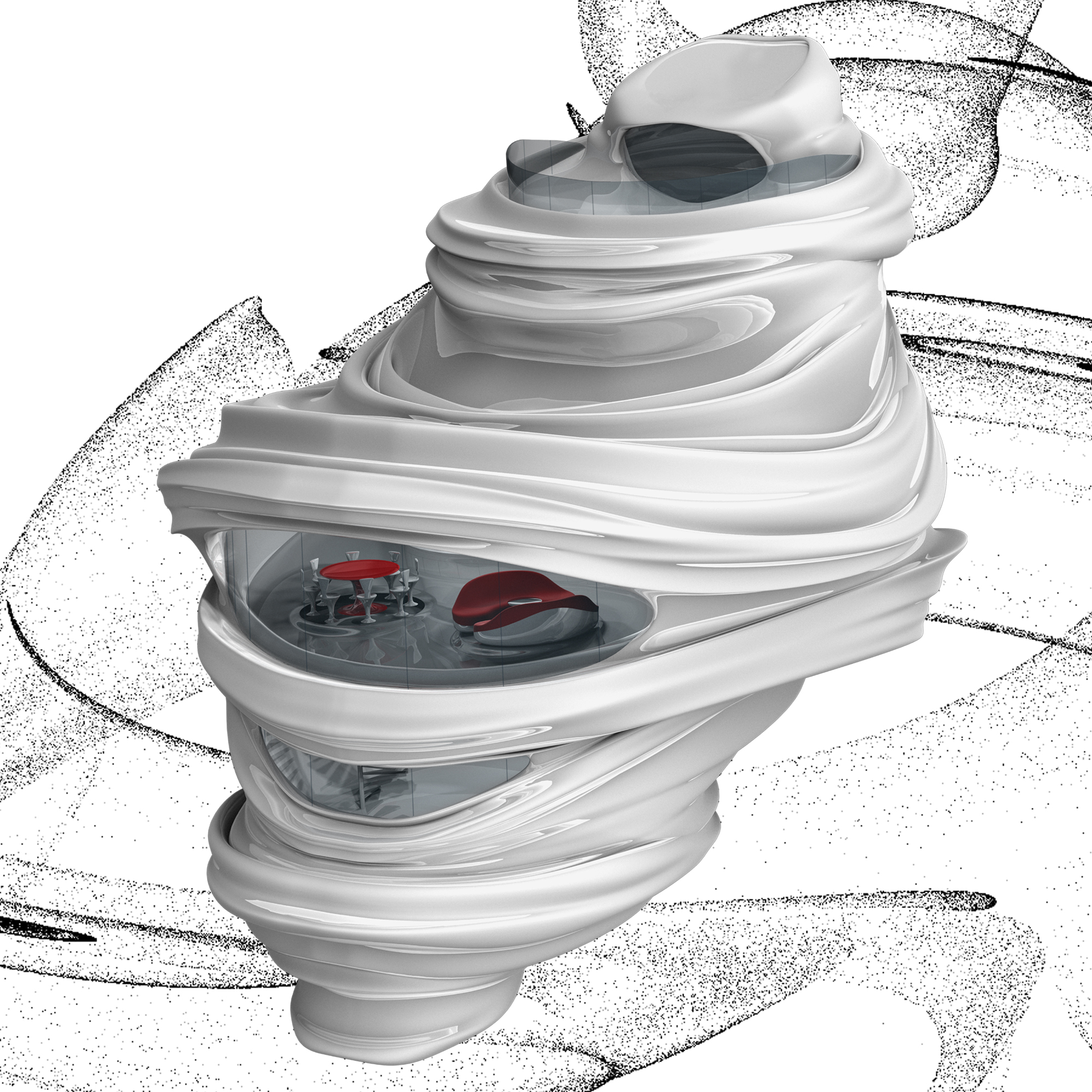
ARCHITEKTURA NACHÁZEJÍCÍ INSPIRACI VE VIRTUÁLNÍ PŘÍRODĚ



Princip

Virtuální příroda se nevytváří klasickým modelováním, kdy všechny tvary se vymodelují ručně jeden po druhém, bez možnosti pozdějších změn jejich vlastností. Tvorba složitých rozsáhlých struktur je tímto způsobem takřka nemožná, či neefektivní. K napodobení přírodních tvarů se používají fraktální funkce. Předpis těchto funkcí bývá jednoduchý, přesto je funkce schopna vygenerovat neomezené množství dat různých hodnot. Princip spočívá v interacích (opakování) a rekurzi (definování objektu pomocí sebe sama). Počáteční vstupní data se vloží do připravené funkce, ta vygeneruje výsledek. Tento výsledek se následně přesune na začátek řetězce a zvonu se nechá propočítat funkcí. Tento proces se několikrát zopakuje, dokud nezískáme potřebné množství sobě podobných dat, která spolu tvoří výsledek – fraktál.



Geometrické fraktály

Efektivnost použití fraktálu se nejlépe ukazuje na geometrických fraktálech, kdy jsou jako vstupní data použity přímo geometrické objety – např. úsečky. Vývoj Kochovy křivky - funkce je definovaná: 1) každou úsečku rozdělí na třetiny, 2) nad prostřední třetinou vytvoří rovnostranný trojúhelník 3) vymaže základnu). Na výsledek se proces aplikuje několikrát po sobě.



Komplexní fraktály

V sedmdesátých letech Benoît Mandelbrot zkoumal vlastnosti fraktálů tvořených komplexními čísly a jejich grafické zobrazení v Gaussově rovině, kde reálná část čísla představovala souřadnici na ose x a imaginární souřadnici na ose y. Nejznámější komplexní fraktál je Mandelbrotova množina. K jejímu určení se používá zobrazení, které každému komplexnímu číslu c přiřazuje určitou posloupnost komplexních čísel zn. Tato posloupnost je určena následujícím rekurzivním předpisem: z0 = 0; zn+1 = zn2 + c. Madelbrotova množina je pak definována jako množina komplexních čísel, pro která je posloupnost omezená podmínkou platící pro všechna n: |zn| ≤ m; kde m je reálné číslo. Dalším oblíbenými fraktály jsou Juliovy množiny. Jsou zapsány stejnou posloupností zn+1 = zn2 + c, pro všechna z z komplexní roviny. Zvolíme jedno libovolné komplexní číslo c, které bude charakterizovat množinu. A nyní pro každý bod komplexní roviny z zjistíme, zda neustálým mocněním z a přičítáním konstanty c diverguje. Pokud nediverguje, patří bod do množiny. V praxi vypadá výpočet velmi snadno: Zkoumané číslo z je umocněno a je k němu přičtena konstanta c. Pokud je výsledek v absolutní hodnotě větší než 2, bod nepatří do množiny. Pokud je menší, zopakuje se výpočet. Jestliže ani po několika iteracích nepřesáhne výsledek hodnotu 2, patří bod do Juliovy množiny. Podle počtu iterací, po kterých absolutní hodnota bodu z překročí 2, lze danému bodu přiřadit barvu a získat tak různé barevné přechody.



Zoom

Množina je tvořena nekonečným počtem bodů. Dovoluje nám to tedy obrazce přibližovat a prolétávat jimi „donekonečna.“ V reálném světě je teoreticky obdobný nekonečný zoom, kdybychom měli neomezenou pozorovací techniku. Můžeme prolétávat vesmírem a přibližovat se ke galaxiím, soustavám, planetám, povrchům, a dále zvětšovat a zvětšovat pomocí mikroskopu s nekonečným přiblížením.



Hyperkomplexní fraktály

Z plošných komplexních fraktálů se do prostoru dostaneme snadno. Do formule místo komplexních čísel použijeme hyperkomplexní čísla. Pokud dvousložkové komplexní číslo mohlo určit bod v rovině, k bodu v prostoru by stačilo číslo trojnožkové – triplex. S touto teorií přisel v polovině 19. století W. R. Hamilton. Triplexy byly distributivní a splňovaly zákony modulů. Stále však vycházely struktury, které obsahovaly netriviální dělitele nuly, tj. nenulové prvky, jejichž součin je roven nule. V takovéto struktuře nelze bez omezení dělit.

Násobení bylo třeba definovat takovým způsobem, aby byly zachovány i další aritmetické zákony známe z klasických číselných oborů: asociativita a komutativnost a násobeni, existence jednotkového prvku, inverzních prvků (tj. možnost děleni) a distributivita nasobení vzhledem ke sčitani. Řešení nalezl v kvaternionech – neboli čtyř-složkových číslech. Takovéto číslo lze obecně zapsat jako:

q = r + a i + b j + c k,

kde r, a, b, c jsou čísla reálná. Mezi imaginárními složkami i, j, k platí vztah poněkud složitější:

i2 = j2 = k2 = -1 i j = k | j k = i | k i = j | j i = -k | k j = -i | i k = -j


Hamilton stanovil i principy pro základní matematické operace, vytvořil skalární a vektorový součin.



Redukce dimenzí

Abychom byli schopny čtyřrozměrný prvek zobrazit ve 3D prostoru, musíme jednu dimenzi ubrat – sloučit. 4D těleso protneme rovinou. V této rovině se jedna složka stane závislou na zbylých třech. K úplnému popsání 4D tělesa pomocí 3D těles je potřeba udělat celou sérii těchto „rovnoběžných“ řezů. V každé řezové rovině 4D objektem vidíme odlišné 3D těleso. Je to totéž, jako když vytváříme vrstevnice. 3D krajinu zobrazujeme pomocí čar ve 2D rovině. Ubereme tedy jednu dimenzi. Při dostatečném počtu vodorovných řezů (vrstevnic) jsme schopni si představit 3D povrch. Jednotlivé vrstevnice můžeme vyřezat z kartónu a navrstvit na sebe. Dostaneme tak 3D model tvořený několika 2D řezy. Naneštěstí je náš okolní svět chápán jako 3D prostor a tak je pro nás obtížné si představit objekt o více dimenzích. Objekt tvořený body Mohou body tvořit povrch objektu? Samozřejmě, záleží pouze na detailu vnímání. Pokud si za bod zvolíme atom, pak vše v našem světě je tvořeno body. Toto můžeme aplikovat na mnohem větší objekty. Za jednotlivé body si zvolíme hvězdy. Z dostatečné vzdálenosti bychom byli schopni určit objekt jevící se jako těleso – galaxii.